Any maths buffs?

Do share.

I'll dig out the code and post it tomorrow. Apologies in advance to anyone who tries to read it...

Either way it suggested that you could get up a 20% gradient with a 50/12 or something which I found a little hard to believe. I made it because I was wondering about the maximum gradient you could get up on a fixie/SS, given that the maximum torque you can apply is based on your body weight, and whether you could base your gear choice off that. There are a bunch of factors I didn't account for in my "model" though and I wonder whether anyone can devise anything better.

So, my guess (and I've been drinking) is that the limit is when the vertical component of the propulsion (rider weight on the pedals causes bike to move forwards and up a slope) is counter balanced by the gain in gravitational potential energy from moving up the slope.

Lower gear = less forward motion (and therefore a smaller vertical component).

ICBA with the maths right now, will see if being sober in the morning helps.

My calculation was purely based on a series of gear ratios. Torque at cranks creates torque at chainrings creates tension in the chain creates torque at the cog creates torque on the ground through the back wheel. The upward component of the force on the ground from the back wheel has to offset the weight of rider and bike.

You could almost certainly do the calculation with energy though... Perhaps comparing the GPE of the rider with the cranks parallel to the ground to GPE of rider and bike with the cranks perpendicular to the ground but further up the slope? That would give you a vertical ascent. Then you can derive a maximum gear ratio based on the ground covered at a given gradient. Interesting idea! I'd be keen to see what you find! Might even do some more calculations myself tomorrow.

Okay, I was too interested and had to do a quick calculation...

GPE down the slope:
Rider is k above the minimum position on the bike (k is one crank length - cranks are parallel with the ground)
Bike and rider at minimum position on the slope
GPE_start = m_rider * g * k

GPE up the slope:
Rider at minimum position on the bike (cranks perpendicular to the ground, riders weight on lower pedal)
Bike and rider distance d up the slope
GPE_end = (m_rider + m_bike) * g * d sin(theta)

d = k / [(1 + m_bike/m_rider) * sin(theta)]

d is (metric) gear inches / 4 - we only considered a quarter revolution of the cranks

For k = 0.175m, m_bike = 10kg, m_rider = 75kg, theta = 20deg, we get d = 0.451m or 17.8 inches

So that's 71.2 gear inches, which is bang on a 43/16 on a 25mm, 700c tyre, a fairly typical fixie gear ratio! How satisfying!

To cycle up a 45 degree slope with the same bike weight, cranks, etc., you only need a 34/26!

Of course I'm ignoring drivetrain losses, loss of traction, what the upper foot is doing, the use of your muscles, etc.

Enjoy this beautiful diagram which definitely clarifies what I've written above.

1 Attachment

Oh do you know Matt Parker? My friend Katie has worked with him a lot

Only from youtube!

https://www.lfgss.com/comments/14103979/

nice.

Does someone fancy checking my working?

I wanted to check my spoke tension meter calibration using tone. Tried measuring the tone and working out the tension from that, but there are too many overtones to reliably know which I should be measuring on the frequency analysis, so I've decided to try working backwards, calculating the theoretical tone, generating that with the laptop and comparing with the spoke tone at the meter-read tension

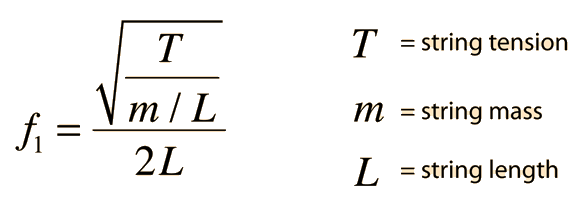
Using this formula, I input values of T=125kgf [Stans recommended spoke tension] x 9.98 [as it should be in newtons], mass per unit length as: π x 0.0009m^2 [1.8.mm spoke] x 8000kg/m^3 [density of stainless steel], L = 0.205m [vibrating length of spoke from nipple interior to outer cross is 205mm].

But I keep getting values of >1hz, which is obviously not right.

Did you forget to square the 0.9mm? Google tells me 270Hz based on the numbers you've given.

Creative solution though. Nice.

I was using millimeters for the 2L! knew it would be something like that.

Although I get about 598hz (tension is actually 1225.83n)

If i was going to buy a hundred lottery tickets, would i be better off getting tickets for 100 different draws, or all for the same draw?

Depends on the rules of the lottery, i.e. what the payout is for a win, and what counts as a win.

e.g if you have 100 "wins" of 3 numbers each you get 100 x £10, but that's a different calculation to 100 wins of 6 numbers each, where a single jackpot is split 100 ways.

You'd need to do an "expected value" calculation (http://www.statisticshowto.com/probability-and-statistics/expected-value/) for each outcome and then compare them.

If you're just counting wins as winning the jackpot (or a share thereof) like a raffle, then your examples are equivalent. (single ticket has 1/100 chance of winning, but your win is 100 times the size in the end).

Also depends on the number of entrants. What are the chances that you're sharing your win with someone else?

(Physicists ht on, maths hat off) But the expected value of a lottery win is so close to zero anyway, nothing you do make much significant difference.

http://datagenetics.com/blog/october22016/index.html

Try that, haven't checked it that closely but when I read it first time it was relevant.

That's not quite relevant as the number of tickets in a lottery isn't finite (I heard a figure that some 20,000 tickets per week pick 1,2,3,4,5,6).

I'm with @Drakien on this, the chance of an individual ticket winning is not affected by other tickets. How much you win may be.

If it were me I'd probably split the 100 tickets over 10 or 20 draws to spread it out rather than spunking it all on one single draw (and suffering the single anticlimax of not winning much). The National Lottery phone app allows easy checking for winning tickets by scanning the QR code on the ticket.

cheers all

I was thinking about the lump sum that people get on retirement, and whether it would be better to spunk it all on a load of lottery tickets or instead spend the same amount on lottery tickets instead of saving for the lump sum.

Vaguely related... I went to a lecture years ago, which went through the statistics of how to maximise your chances of winning the maximum amount with a winning ticket, going through things like how people are drawn to certain patterns when choosing etc. at the end of the lecture he gave the six numbers which would maximise the return, the kicker was that he had given that same lecture to thousands of people so those six were no longer true!

Also saw a lecture on the mechanics of juggling, that blew my mind.

mechanics of juggling

Siteswap notation? It's fascinating stuff. https://en.wikipedia.org/wiki/Siteswap

Yep, thats the stuff, was straightforward for 2 or 3 balls, but once he got over 5 it was crazy, helped by the fact that the lecturer was juggling through the lecture. Just realised these lectures were nearly 20 years ago, that makes me feel old, think it might have been Colin Wright who gave the lecture actually.

Problem that I came across. Leibniz thought that rolling two die and getting 11 was as likely as getting 12. If he took two die and started rolling them,

"how many 2d6 rolls is Liebniz expected to need before he can say they're not [equally likely]?"

I bodged an answer with Python but maybe a proper stats/Bayesian person can give a real answer?

Stats is not my preferred part of maths but surely you'd need some form of confidence interval to give bounds in order to be able to answer that question?

I may have misunderstood the question and be massively oversimplifying, but you wouldn’t actually need to roll any dice to calculate the expected probabilities of the two outcomes would you?

With two die there’s a total of possible 36 outcomes, only one of which produces 12, whereas there are two outcomes resulting in 11, so given infinite rolls you’d expect to see twice as many 11’s rolled as 12’s right?

Dices.

Grammar buffs thread >>>>>>>>>>>>>>