Any question answered...

They're different things aren't they. Lines of longitude always circle the entire globe and always pass through the poles. Lines of latitude are always parallel to each other and so never meet and change in size.

Here's one of the worst diagrams I've ever seen (note latitude lines never meet):

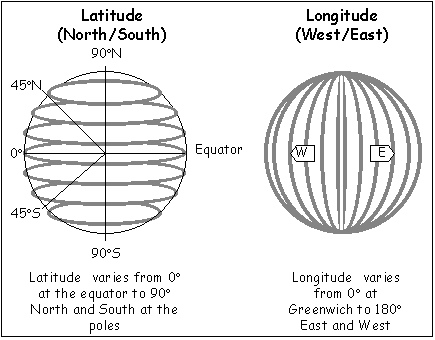
If you're asking why we define positions using one converging coordinate and one non-converging coordinate then it's more complicated but basically it's mathematically nice/convenient especially for calculating distances on the surface. It's effectively the spherical coordinate system. We could use Cartesian (x, y, z) coordinates but they're horrible for spheres (great on a flat plane though). We could use cylindrical coordinates (r, θ, z) and that would be okay but the z is less convenient than a latitude (great if you live on a disc - we use them for galactic coordinates).

One or the other must converge, because we're on a curved surface. As we are on a rotating body there is a good reason to align the symmetry of the body as it rotates to the symmetry of the coordinate system we use. This is why we choose the lines of longitude (the meridians) to converge and maintain (local) parallelism between lines of latitude.

If you really wanted, you could arbitrarily define an east and west poles, with converging lines of longitude. It would be a pain in the arse, but you could do it. However, the north and south poles would still be important because they arise from the symmetry.

If you want to talk more about the curved geometry then the maths thread is a better place I suspect.